Mata kuliah saya diantaranya aljabar Linier. waduh susah dah. dengan latar belakang sms.. akibat googling.. saya mendapat kan jawaban.. tra tar.
To find the inverse of matrix A, using Gauss-Jordan elimination, we must find a sequence of elementary row operations that reduces A to the identity and than perform the same operations on In to obtain A-1.
Inverse of 2 x 2 matrices
Example 1: Find the inverse of
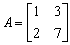
Solution:
Step 1: Adjoin the identity matrix to the right side of A: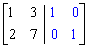
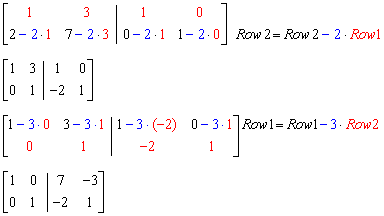
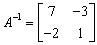
Not invertible matrix
If A is not invertible, then, a zero row will show up on the left side.Example 2: Find the inverse of
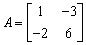
Solution:
Step 1: Adjoin the identity matrix to the right side of A: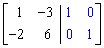
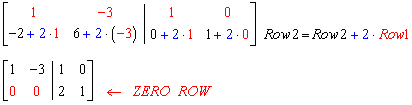
Inverse of 3 x 3 matrices
Example 1: Find the inverse of
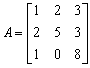
Solution:
Step 1: Adjoin the identity matrix to the right side of A: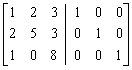
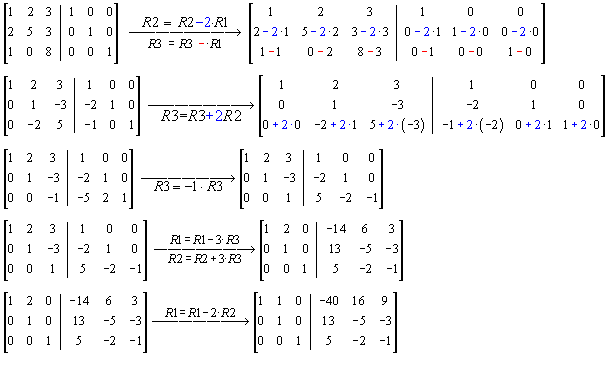


No comments:
Post a Comment